3: Resistencia al corte de los suelos
3.1: Criterio de rotura de Mohr – Coulomb
3.1.1. Introducción: fuerzas que actúan sobre el terreno
Resulta necesario realizar una cierta introducción general sobre las fuerzas que actúan en el terreno, para poder definir posteriormente los descriptores geotécnicos que se refieren a la resistencia al corte del suelo.
Las solicitaciones a las que está sometido el terreno derivan de un origen fundamental: el campo gravitatorio. No obstante, es tradicional dividirlas en dos clases, en función de la persistencia o no de las mismas. Así, se acostumbran a considerar los siguientes grupos de fuerzas:
– Gravitatorias, en sentido estricto, causantes de las acciones derivadas de las masas consideradas permanentes: peso propio del terreno, sobrecarga litostática, empujes de confinamiento, empujes hidrostáticos…
– Cargas externas, generadas por masas cuya actuación se considera variable en el análisis geotécnico: sobrecargas debidas a una cimentación, empujes que se generan por la inestabilidad en un talud, gradientes hidráulicos…
En un concepto fundamental tal vez algo simplista, los problemas a resolver en geotecnia se resumen en la determinación de la relación entre las tensiones externas y la deformación del terreno o, llegado al extremo, su capacidad última en rotura.
Dado que, también en sentido estricto, el suelo es un material anisótropo, heterogéneo, y cuya deformabilidad no se adecúa al modelo de la elasticidad, el problema podría resultar en exceso complejo para abordar soluciones en la mayoría de los casos cotidianos que debe resolver la ingeniería geológica. Por esta razón es razonable adoptar una aproximación simplificada, y considerar en ciertas ocasiones que el suelo se comporta de forma asimilable al modelo de deformación elástica, que dentro de ciertos límites el suelo puede considerarse homogéneo, y que sus propiedades mecánicas pueden estimarse independientes de la dirección de los esfuerzos aplicados.
Muy posiblemente estas tres simplificaciones permitan resolver la gran mayoría de problemas geotécnicos habituales, sin que el error que de las mismas se deriva penalice de forma sensible la seguridad de la obra o el coste de la misma.
3.1.2. Resistencia al corte de los suelos: criterio de Mohr – Coulomb, ángulo de rozamiento y cohesión
Tal vez la contribución más relevante de Charles A. de Coulomb se relacione con su ámbito de físico teórico al postular la ley de interacción (atracción / repulsión) entre cargas eléctricas; no obstante, el trabajo cotidiano del Coulomb versaba sobre aspectos más mundanos del conocimiento. Como ingeniero militar participó en el diseño de varias fortalezas, ocupándose de forma reiterada del proyecto de estructuras de contención.
Basándose substancialmente en trabajos precedentes de Gullaume Amontons sobre el rozamiento entre sólidos, Coulomb propuso una teoría para explicar la presión de tierras sobre un muro, publicada en 1776, que enfoca el problema de empujes sobre muros considerando que los mismos se pueden asimilar a unas cuñas de falla.
El fundamento de dicho trabajo consiste en valorar la resistencia al corte del suelo en base a la siguiente expresión:
τ = c + σ tg φ
o, lo que es lo mismo, que la resistencia del suelo ante el esfuerzo cortante es la suma de su cohesión y del rozamiento en el plano de rotura, y que tal rozamiento viene determinado por el producto de la tensión normal ([1]) a dicho plano por la tangente del ángulo de rozamiento interno del material.
Si bien el concepto cohesión ([2]) es intuitivamente asimilable, el concepto rozamiento requiere probablemente una pequeña reflexión adicional. Nótese que la fuerza de rozamiento depende de la existencia de una tensión perpendicular a la fuerza tangencial o de corte, y que en caso que dicha fuerza normal fuese nula, el rozamiento sería también nulo (sea cual fuere el ángulo de rozamiento interno).
Conviene ahora aclarar de forma sucinta el concepto «ángulo de rozamiento interno».
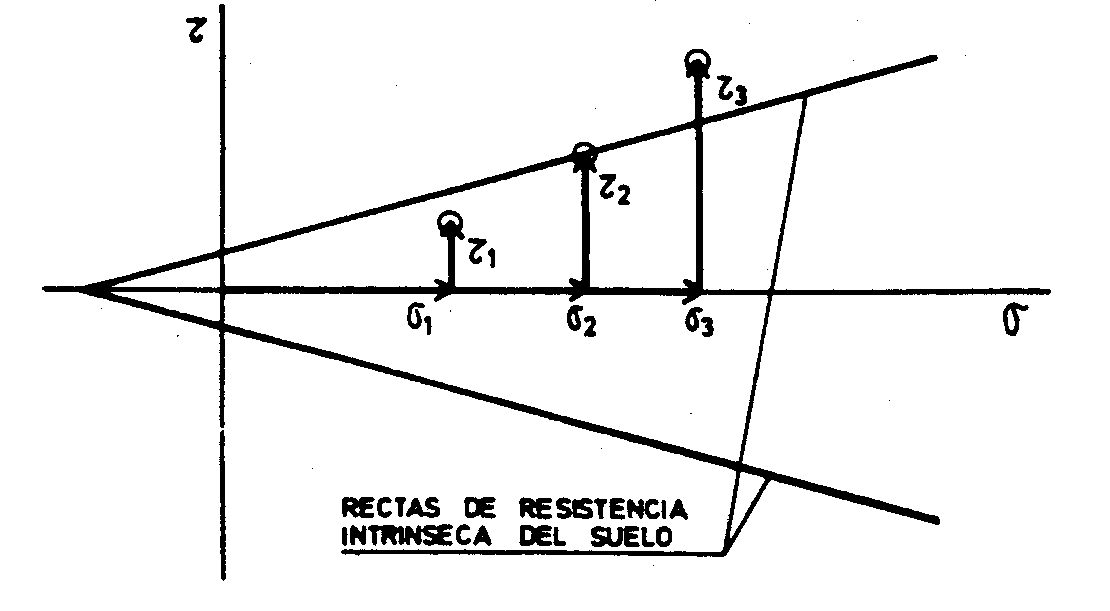
El postulado general del modelo de Coulomb propone un criterio de rotura que se representa en el plano σ – τ (esfuerzo normal y esfuerzo tangencial respectivamente) por dos rectas que se denominan “rectas de resistencia intrínseca” del suelo, tal como muestra la siguiente figura:
La combinación de tensiones normales y tangenciales que esté comprendida entre las dos rectas corresponde a un estado de tensiones posible en el que puede encontrarse el suelo. Los puntos que resulten de combinaciones de tensiones situadas en las rectas corresponden al límite de rotura, y los exteriores definirán estados de tensiones más allá del límite de rotura y por lo tanto en los que no puede encontrarse el suelo.
Resulta evidente que para un caso en que el valor de la tensión normal (σ) fuera nulo, la fuerza resistente debida al rozamiento sería también nula, y que por lo tanto la única fuerza responsable de la resistencia del suelo sería la cohesión, que toma en consecuencia el valor de la ordenada en el origen de la gráfica σ – τ.
A partir de este punto, el incremento de σ conlleva un incremento directamente proporcional de la resistencia al corte que se suma a la cohesión, y cuyo valor es igual al producto del valor de σ en cada punto por la tangente del ángulo que forma la recta de resistencia intrínseca del suelo con el eje σ. Dicho ángulo se denomina, pues, ángulo de rozamiento interno.
Una analogía mecánica sencilla que permite visualizar el significado de este ángulo de rozamiento interno consiste en considerar un plano inclinado de inclinación variable (tal cual el plano de rotura) sobre el cual se dispone un sólido (pongamos de una geometría regular… un paralelepípedo por ejemplo); partiendo de la horizontal, se incrementa progresivamente el ángulo del plano inclinado hasta que el sólido inicia el deslizamiento:
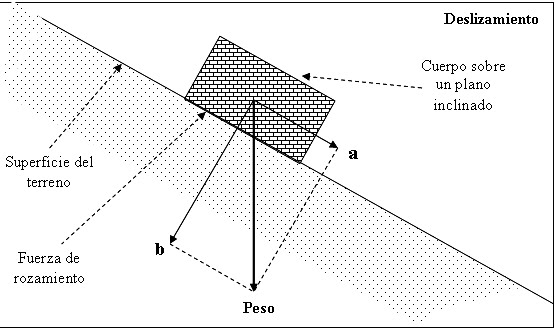
El vector peso puede ser descompuesto en dos vectores en relación al plano: a (paralelo al plano, y correspondiente a la fuerza tangenciáo) y b (perpendicular al mismo, correspondiente a la fuerza normal.) Si a supera a la fuerza de rozamiento (b · tg φ), el cuerpo iniciará el deslizamiento pendiente abajo cuando la inclinación del plano sea i = φ.
Esta teoría general de sólidos podemos extenderla a los suelos considerando que el rozamiento entre granos aislados corresponde al ángulo φ. No obstante, la movilización de los granos a pequeña escala no depende solo de su rozamiento mutuo, si no de la traslación necesaria entre las partículas para posibilitar el movimiento relativo de dos masas de suelo que deslizan una respecto a la otra, separadas por una superficie de rotura (debido a lo cual el rozamiento interno del suelo es superior al rozamiento entre partículas).
Por esta razón, la forma en la que las partículas que forman el suelo se encuentren dispuestas unas respecto a otras (el empaquetamiento) es un factor fundamental en el valor del rozamiento interno del mismo: cuanto más compacto sea dicho empaquetamiento (y por tanto, cuanto más denso sea el suelo), mayor será su rozamiento interno, y en consecuencia su resistencia al corte.
PS. si te ha sido útil este post, no olvides visitar a alguno de nuestros anunciantes… este sitio se edita y mantiene de forma altruista, así nos puedes ayudar a costear el alojamiento.
[1] perpendicular al esfuerzo cortante
[2] entendida en sentido estricto como la fuerza que mantiene la unión de las partes constituyentes de un todo, y para el caso de suelos, la fuerza que atrae entre sí a las partículas que lo conforman.








Que parámetro de resistencia al cortante (criterio de MOHR), considera como el menos importante en los
rellenos o suelos que se tendrían que sostenerse mediante el diseño de un muro de contención.
lo que es yo, ninguno de los dos, como opinión personal, ambos son importantes
Explique el criterio de falla idealizado en suelo, y haga énfasis en el esfuerzo crítico y esfuerzo residual.
a ver si me jubilo y tengo tiempo para todo lo que me piden, especialmente los que lo hacen con buena educación… caramba, que este blog es gratis.
🙁